高考语文六模试题题号一二三四总分得分一、选择题（本大题共10小题，共30。0分）1。-的倒数是（）A。B。-C。D。-2。如图，是平切一个圆球，切去一部份后得到的几何体，它的俯瞰图是（）A。B。C。D。abAcB3。如图，直线与直线交于点，与直线交于点，∠1=110°∠2=40°acA，，若直线，保持不动，绕点逆秒针bbcb旋转直线，使∥，则直线逆秒针旋转度数可以是（）A。25°B。30°C。35°D。40°ABOB-10y=kx4。如图，在等腰△中，点（，），若正比列函数Ak的图像经过点，则的值为（）A。-B。-C。-D。5。下述估算正确的是（）22423x+x=4xx-1=x-1A。B。（）4322426xy÷2x=3x-xy=xyC。（）（）D。（）RtABCC=90°DEABAB△∠6。如图，在中，，直线垂直平分，交DACEDDH⊥ACHBC=3于点，交于点，过点作于点，已知AC=4EH，，则的长为（）第1页，共20页A。

B。C。D。y=2x+2x3y7。直线沿轴向左平移个单位宽度后与轴的交点座标是（）02040-408A。（，）B。（，）C。（，）D。（，）8。如图，在周长为2的正圆形ABCD中，以对角线AC为一边作矩形AEFC，联接AF交BC于点G，则BG的长为（）A。2-2B。2-1C。D。19。如图，四边形ABCD是⊙O的内接四边形，．若∠BAC=45°，∠B=105°，则下述方程创立的是（）A。AB=CDB。AB=CDC。AB=CDD。AB=CD2A-6yB2yy=ax+bx+ca≠0Cxy10。已知两点（，），（，）均在抛物线（）上，点（，1200y≥yyx）是该抛物线的顶点，若＞，则的取值范围是（）0120x-6x-2-6x-2-2x2A。＜B。＜C。＜＜D。＜＜0000412。0二、填空题（本大题共小题，共分）-0-10。

121121112π______11。在实数，，，，，中，无理数的个数为个．12。正六边形的一个中心角为36度，这么这个正六边形的一个外角等于______度．y=k0RtABOOAD-5m13。如图，反比列函数（＜）的图像经过△斜边的中点（，），ABCAOC15k______且与直线相交于点．已知△的面积为，则的值为．第2页，共20页ABCDAB=15AD=10PAB14。如图，在圆形中，，，点是边上任意一点（不与A点重合），联接PD，以线段PD为△DPQQPD直角边作等边直角（点在直线左侧），∠DPQ=90°BQBQ______，联接，则的最小值为．15。0三、计算题（本大题共小题，共分）-x-2÷15。通分：（）四、解答题（本大题共10小题，共73。0分）2019-π0||-16。估算：（）+ABCMACAB17。如图，已知△，为上一点，请用尺规在NBN=MN边上找一点，使．（保留画图痕迹）第3页，共20页BECFBE=CFABDEACDF18。

已知：如图，点，，，在同一条直线上，且，∥，∥，求证：AB=DE．19。为了解朝阳社区20～60岁市民最喜欢的支付形式，某兴趣小组对社区内该年纪段的部分居民展开了随机问卷调查（每人只能其中一项）并将调查数据整理后勾画成两幅不完整的统计图．请依照图中信息解答下述问题．1______C（）参与问卷调查的总人数为，参与调查的人中选择．现金支付的人数______为；2（）在此次调查中，哪种支付方法的选择人数多于各支付方法选择人数的平均数？320-608000（）该社区中岁的村民约人，计算值那些人中最喜欢陌陌支付形式的人数．第4页，共20页20。随着人们对生活环境的要求逐步提升，环境保护问题遭到越来越多人的关注，环保宣传也随处可见．如图，小云想要检测窗前的环保宣传牌AB的高度，她发觉晚上阳光正好从阳台的最低点C处射进卧室的地板射进卧室的地板F处，下午阳光正好从阳台的最高点处射进卧室的地板E处，小云测得阳台距地面的高度OD=1m，CD=1。5mOE=1mOF=3mAB窗高，并测得，．请依照以上检测数据，求环保宣传牌的高度．21。

咸阳樱桃集中中国樱桃之优，素以肉质鲜亮，果大皮薄，汁多味甜，核软鲜美，籽肥渣少，品质优良等特性见称，久居中国五大名榴之冠，被列为果中珍品，历来是唐代臣子的贡品，遍及九州，现政府想将某樱桃基地规模扩大，计划栽种红籽樱桃和白籽樱桃共60亩，有关数据如表：////成本（亿元亩）销售额（亿元亩）红籽樱桃4。86白籽樱桃451xyyx（）设养殖红籽樱桃亩，两种樱桃的总利润为亿元，求关于的函数解析=-式（利润销售额成本）．2260（）若计划投入的成本的总金额不超过亿元，要使获得的利润最大，基地应栽种红籽樱桃和白籽樱桃分别多少亩？20181216422。年月日，南宁市轻轨号线带着华美的外表和深厚的文化开通试营运，火车车箱的Tiffany蓝与车箱的底部及肩膀的科技感爆棚的银色相互搭配，被首批试乘的乘客称为“仙女专列”．小华和小丽借助新年放暑假间进行了南京居民对轻轨4号线的满意度的调查，如图是长春轻轨四号线南端的五站路线图，小华和小丽第5页，共20页分别在飞天路、东长安街、神舟大街这三站中随机选定一站作为调查的站点．1____（）小华选定的站点的飞天路的机率为；2（）请用列表或画树形图的方式，求小华和小丽选定的站点相邻的机率．ABCD⊙OBD⊙OAE⊥CDCD23。

如图，四边形内接于，是的半径，交的延长线于点EDA∠BDE。，平分⑴求证：AE是⊙O的切线；⑵AE＝4cm，CD＝6cm，求AD的长。2Cy=ax+bx+3xA-30yCM-224。抛物线1：与轴交于（，）两点，与轴交于点，点（，3）是抛物线上一点．1C（）求抛物线1的表达式．2CCyABMyA（）若抛物线2关于1关于轴对称，点、、关于轴的对称分别为′、BMM⊥xEACDxP′、′．过′轴于点，交直线′于点，在轴上是否存在点，ADPABCP是促使以′、、为顶点的三角形与△′相似？若存在，恳请出点的座标；若不存在，请说明理由．第6页，共20页25。问题提出1ABCBC=2ABCB60°（）如图①，在△中，，将△绕点顺秒针旋转得到ABCCC=______△′′′，则′；问题探究2ABCAB=BC=3ABC=30°PABCPA△∠△（）如图②，在中，，，点为内一点，联接PBPCPA+PB+PC、、，求的最小值，并说明理由；问题解决3ABCDADBCAB=6AD=4ABC=BCD=60°（）如图③，在四边形中，∥，，，∠∠．在ABCD∠APD=120°BPCPQ△BPC四边形内部有一点，满足，联接、，点为内的任意一点，是否存在一点P和一点Q，致使PQ+BQ+CQ有最小值？若存在，恳请出这个最小值；若不存在，请说明理由．第7页，共20页第8页，共20页答案和解析B1。

【答案】--【解析】解：的倒数是：．B故选：．直接借助倒数的定义得出答案．此题主要考查了倒数，正确掌握倒数的定义是解题关键．A2。【答案】【解析】解：从里面看可得到一个圆环的图形，上面的圆画虚线．A故选：．平切一个圆球，切去一部份后得到的几何体后，找到从里面看所得到的图形即可．本题考查了三视图的知识，俯瞰图是从物体的前面看得到的视图，注意看得到的棱画实线．B3。【答案】b【解析】解：如图，旋转到直线′，∵∠1=110°，∴∠DAE=180°-110°=70°，∵∠EAC=20°，∴∠DAC=70°-20°=50°，∵∠2=50°，∴∠2=∠DAC，∴c∥b直线直线′，bA30°bc即当直线绕点逆秒针旋转时，直线与直线平行，B故选：．按照同位角相等，两直线平行推出即可．本题考查了平行线的判断，旋转的性质的应用，能熟记平行线的判断是解此题的关键．A4。【答案】ABOB-10【解析】解：∵△为等腰三角形，且点的座标是（，），∴A-点的座标为（，），∵y=kxA正比列函数的图像经过点，∴=-k，第9页，共20页∴k=-．A故选：．按照等腰三角形的性质结合点B的座标即可得出点A的座标，再由点A的座标借助正k比列函数图像上点的座标特点即可求出值，此题得解．本题考查了等腰三角形的性质以及正比列函数图像上点的座标特点，按照等腰三角形的性质求出点A的座标是解题的关键．D5。

【答案】A=4x2【解析】解：、原式，不符合题意；2B、原式=x-2x+1，不符合题意；C、原式=3xy，不符合题意；42D、原式=xy，符合题意，D故选：．各项估算得到结果，即可做出判定．此题考查了多项式的混和运算，熟练把握运算法则是解本题的关键．C6。【答案】RtABCC=90°BC=3AC=4【解析】解：在△中，∠，，，AB=5∴，∵直线DE垂直平分AB，AE=BEAD=AB=2。5∴，，∵DH⊥AC，DHBC∴∥，AH=CH=AC=2∴，ADE=C=90°A=A∵∠∠，∠∠，ADEACB∴△∽△，∴=，∴=，AE=∴，∴HE=AE-AH=，C故选：．AB=5AE=BEAD=AB=2。5按照勾股定律得到，按照线段垂直平分线的性质得到，，按照三角形的中位线的性质得到AH=CH=AC=2，按照相像三角形的性质得到AE=，于是得到推论．本题考查了线段垂直平分线的性质，相像三角形的判断和性质，正确的做出辅助线是解题的关键．D7。

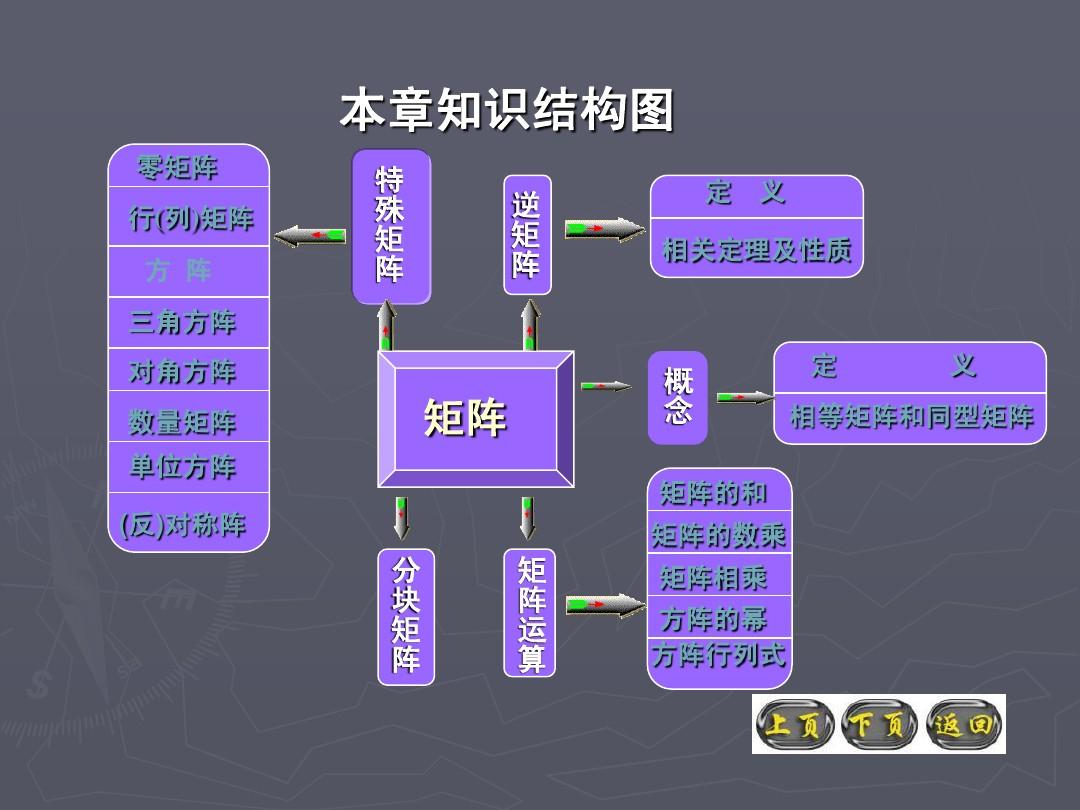
【答案】∵y=2x+2x3【解析】解：直线沿轴向左平移个单位宽度，∴y=2x+3+2y=2x+8平移后的解析式为：（），即，第10页，共20页当x=0，则y=8，∴y08平移后直线与轴的交点座标为：（，）．D故选：．y借助一次函数平移规律得出平移后解析式，从而得出图像与轴的交点．此题主要考查了一次函数图像与几何变换，得出平移后解析式是解题关键．A8。【答案】∵ABCD【解析】解：四边形是正圆形，AC=AB∴，∵四边形AEFC是矩形，∴CF=AC=AB，ABCD∵∥，ABGFCG∴△∽△，∴==，即=，解得，BG=2-2，A故选：．AC=ABCF=ACABGFCG按照正圆形的性质得到，按照矩形的性质得到，证明△∽△，按照相像三角形的性质列式估算即可．本题考查的是相像三角形的判断和性质、正圆形的性质、菱形的性质，把握相像三角形的判断定律和性质定律是解题的关键．B9。【答案】ACBDK【解析】解：如图设交于．∵=网校头条，ACD=BDC=BAC=45°∴∠∠∠，∴∠DKC=90°，∵∠BAC=∠DCK=45°，ABCD∴∥，ABC+BCD=180°∴∠∠，ABC=105°∵∠，∴∠DCB=75°，∠ACB=30°，∵∠CKB=90°，∴CK=BK，∵∠KAB=∠KDC，∠AKB=∠DKC，AKBDKC∴△∽△，∴=，AB=AB∴，B故选：．ACBDK△CBKRt△∠BCK=30°KC=BK如图设交于．首先证明的，，推出，再借助第11页，共20页相像三角形的性质解决问题即可．本题考查圆内接四边形，圆周角定律，相像三角形的判断和性质等知识，解题的关键是熟练把握基本知识，属于高考常考题型．B10。

【答案】∵Cxyy≥yy【解析】解：点（，）是该抛物线的顶点．且＞，00012∴a0x≤-6-6x2＜，或＜＜，00∴x--62-x0（）＜0，∴x-20＜，∴x≤-6x-6x-2或＜＜，00∴x0＜-2B故选：．a0AByy≤yA由抛物线顶点纵座标最大可得出＜，对称轴在、之间，结合1＜20可得出点Bx≤-6-6x2x≤-6x--6到对称轴的距离大于点到对称轴的距离，得到或＜＜，即或（0000）＜2-x0，解之即可得出推论．y≥yyx-本题考查了二次函数的性质以及二次函数图像上点的座标特点，由＞找出（0120-6）＜2-x0是解题的关键．311。【答案】0。121121112π3【解析】解：无理数有：，，共个．故答案为：3无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的合称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．π2π此题主要考查了无理数的定义，其中中学范围内学习的无理数有：，等；开方开不尽的数；以及像0。

1010010001…，等有这样规律的数．14412。【答案】【解析】解：因为正六边形的中心角等于36°，360÷36°=10，所以正六边形为正10边形，又由于其内角和为360°，所以其内角为360÷10=36°，其每位顶角为180°-36°=144°．故答案为144．按照正六边形的中心角为36°，求出正六边形的边数，再求出其每位内角，即可按照内角和内角的和为180度求出每位顶角的度数．本题考查中学生对正六边形的概念把握和估算的能力．解答这类题常常一些中学生因对正多边形的基本知识不明晰，将六边形的中心角和内角、内角混淆．-1013。【答案】RtABOOAD-5m【解析】解：∵△斜边的中点（，），A-102m∴（，），∴OB=10，AOC15∵△的面积为，∴ACBO=15•，AC=3∴．∴BC=2m-3，第12页，共20页∴C-102m-3（，），y=k0RtABOOADAB∵反比列函数（＜）的图像经过△斜边的中点，且与直线相交于C点．∴k=-102m-3=-5m（），∴k=-10，故答案为-10．先表示出点A的座标，借助三角形的面积公式求出AC，即可表示出C的座标，之后根据反比列函数图像上点的座标特点即可求得k的值．本题主要考查了反比列函数系数k的几何意义，一次函数图像上点的座标特点，反比列函数图像上点的座标特点，解题的关键是表示出点C的座标．14。

【答案】QQE⊥ABEEP【解析】解：如图所示，过作于，在上截取EF=EQ，联接QF，∵△DPQ是等边直角三角形，四边形ABCD是圆形，∴DP=PQ，∠A=∠PEQ，∠ADP=∠EPQ，ADPEPQAAS∴△≌△（），AP=QE=FEAD=PE=10∴，，AF=PE=10∴（定值），又∵△EFQ是等边直角三角形，∴∠QFE=45°，即FQ与FB的倾角仍然为45°，BQ⊥FQBQ如图，当时，的长最小，此时，△BQF是等边直角三角形，又∵QE⊥BF，∴BE=EF=QE=AP，又∵PE=10，∴BE=AP==，∴BF=5，∴BQ=cos45°×BF=，即BQ的最小值为，故答案为：．QQE⊥ABEEPEF=EQQF过作于，在上截取，联接，根据全等三角形的性质，即可AF=PE=10△EFQFQFB得到（定值），根据是等边直角三角形，可得与的倾角仍然45°BQ⊥FQBQ△BQF为，从而得到当时，的长最小，依据是等边直角三角形，即可得到BQ的厚度．本题主要考查了圆形的性质，全等三角形的判断与性质以及等边直角三角形的性质的运用，解决问题的关键是作辅助线构造全等三角形以及等边直角三角形．15。

【答案】解：原式=÷=•第13页，共20页=x+12-x（）（）2=-x+x+2【解析】根据多项式的运算法则即可求出答案．本题考查分式的运算，解题的关键是熟练运用多项式的运算法则，本题属于基础题型．16。【答案】解：原式=1+2--3=3-4．【解析】直接借助二次根式的性质、零指数幂的性质、绝对值的性质分别通分得出答案．此题主要考查了实数运算，正确通分各数是解题关键．BMEFABNMNN17。【答案】解：如图，作线段的垂直平分线交于，联接，点即为所求．BMEFABNMNN【解析】如图，作线段的垂直平分线交于，联接，点即为所求．-本题考查画图复杂画图，解题的关键是熟练把握五种基本画图，属于高考常考题型．18。【答案】证明：∵BE=CF，∴BE+EC=CF+EC，即BC=EF，ABDE∵∥，∴∠B=∠DEF，ACDF∵∥，ACB=F∴∠∠，ABCDEF在△和△中，，ABCDEFASA∴△≌△（），AB=DE∴．【解析】先求出BC=EF，再依照两直线平行，同位角相等求出∠B=∠DEF，∠ACB=∠F，ABCDEF之后借助“角边角”证明△和△全等，按照全等三角形对应边相等证明即可．本题考查了全等三角形的判断与性质，平行线的性质，熟练把握三角形全等的判断方式是解题的关键．5007519。

【答案】1200÷40%=500500×15%=75【解析】解：（）人，人，故答案为：500，75．2C15%D10%25%（）组占，组占均大于，现金支付、其它支付方法的选择人数多于各支付方法选择人数的平均数．38000×40%=3200（）人答：那些人中最喜欢陌陌支付形式的人数为3200人．第14页，共20页140%200（）扇形统计图中得使用支付宝的占，从条形统计图中得使用支付宝的有人，可求调查的人数，再用调查的人数除以选择C所占的比15%即可，2（）哪种支付方法的选择人数多于各支付方法选择人数的平均数，就看哪种支付方法所占的比大于25%即可，考查条形统计图、扇形统计图的特征及制做方式，把握两种统计图在表示一组数据的优点和统计图中的数据之间的关系是解决问题的关键．20。【答案】解：∵DO⊥BF，∴∠DOE=90°，∵OD=1m，OE=1m，∴∠DEB=45°，ABBF∵⊥，∴∠BAE=45°，AB=BE∴，设AB=EB=xm，ABBFCOBF∵⊥，⊥，ABCO∴∥，ABFCOF∴△∽△，∴=，=，解得：x=10．经检验：x=10是原多项式的解．答：AB的高度是10m．【解析】首先按照DO=OE=0。

8m，可得∠DEB=45°，之后证明AB=BE，再证明ABFCOF=△∽△，可得，然后代入数值可得多项式，解出多项式即可得到答案．此题主要考查了相像三角形的判断与性质，解决问题的关键是求出AB=BE，按照相像ABFCOF三角形的判断方式证明△∽△．121。【答案】解：（）由题意可得，y=6-4。8x+5-460-x=0。2x+60（）（）（），yxy=0。2x+60即关于的函数关系式是；2（）由题意可得，4。8x+460-x≤260（），解得，x≤50，y=0。2x+60∵，∴x=50yy=7060-x=10当时，取得最大值，此时，，答：要使获得的利润最大，基地应种红籽樱桃50亩，白籽樱桃10亩．1yx【解析】（）按照题意和表格中的数据可以得到关于的函数关系式；21（）按照题意可以的相应的不方程，再依照（）中的函数关系式即可解答本题．本题考查一次函数的应用、一元一次不方程的应用，解答本题的关键是明晰题意，找出所求问题须要的条件，借助一次函数的性质和不方程的性质解答．22。

【答案】第15页，共20页1【解析】解：（）小华选定的站点的飞天路的机率为；故答案为；2ABC（）画树形图为：（用、、分别表示飞天路、东长安街、神舟大街这三站）94共有种等可能的结果数，其中小华和小丽选定的站点相邻的结果数为，小华和小丽选定的站点相邻的机率=。1（）直接借助机率公式估算；2ABC（）画树形图（用、、分别表示飞天路、东长安街、神舟大街这三站）展示所有9种等可能的结果数，找出小华和小丽选定的站点相邻的结果数，之后按照机率公式计算．n本题考查了列表法与树形图法：借助列表法或树形图法展示所有等可能的结果，再从ABmAB中选出符合风波或的结果数量，之后借助机率公式估算风波或风波的机率．1OA23。【答案】（）证明：联结．∵OA=OD，∴∠ODA=∠OAD．∵DA平分∠BDE，∴∠ODA=∠EDA．∴∠OAD=∠EDA，∴EC∥OA．AECD∵⊥，∴OA⊥AE．∵点A在⊙O上，AEO∴是⊙的切线．2OOF⊥CDF（）解：过点作，垂足为点．∵∠OAE=∠AED=∠OFD=90°∴四边形AOFE是方形．∴OF=AE=4cm．EF=OA，又∵OF⊥CD，∴DF=CD=3cm．在Rt△ODF中，OD==5cm，即⊙O的直径为10cm，∴EF=OA=5cm，∴ED=EF-DF=5-3=2cm，RtAEDAD==2在△中，．【解析】本题考查了等边三角形的性质，垂径定律，平行线的判断和性质，切线的判断和性质，勾股定律的应用等，熟练把握性质定律是解题的关键．1∠ODA=∠OAD∠OAD=∠EDAEC∥OA（）按照等腰对等角得出，从而得出，证得，因而证得AE⊥OA，即可证得AE是⊙O的切线；2OOF⊥CDFAOFEOF=AE=4cm（）过点作，垂足为点．因而证得四边形是圆形，得出第16页，共20页，按照垂径定律得出DF=CD=3cm，在Rt△ODF中，按照勾股定律即可求得⊙O的半径，得出ED，按照勾股定律即可求得AD．1AM24。

【答案】解：（）将点、的座标代入函数表达式得：，解得：，2Cy=-x-2x+3故抛物线1的表达式为：；2A-30B10C03M-23B-10（）由题意得：点（，）、（，）、（，）、（，）、′（，）A30D21、′（，），（，），AB=2AC=3BC=AD=则′，，′，′，①当点P在直线AC的右侧时，当点P在DM′左侧时，ADPABC′、、为顶点的三角形与△′相似，ABCADP则△′∽△′，则，AP=3即：，解得：′，P00故点（，），当点P在DM′左侧时，PP0同理可得点（′）（，）；②当点P在直线AC的左侧时，ABCDAP则△′∽△′″，PP3+0同理可得：点（″）（，）；P0003+0综上，点的座标为（，）或（，）或（，）．1AM【解析】（）将点、的座标代入函数表达式，即可求解；2PACPAC（）分当点在直线的两侧、点在直线的两侧两种情况，分别求解即可．2本题考查的是二次函数综合运用，涉及到图形的平移、三角形相像等，其中（），要注意分类求解，防止遗漏．225。

【答案】第17页，共20页1【解析】解：（）如图①，由性质的旋转可知：△BCC′是等腰三角形，∴CC=BC=2′，2故答案为．2ABPBABPB60°BFEPFECBHEC（）如图②，将△绕点逆秒针旋转得到△，联接，，作⊥于H．由旋转的性质可知：△PBF是等腰三角形，∴PB=PF，∵PA=EF，∴PA+PB+PC=PC+PF+EF，∵PC+PF+EF≥EC，∴PFECPA+PB+PC当，在直线上时，的值最小，易证BC=BE=BA=3，∠CBE=120°，∵BH⊥EC，∴∠CBH=∠EBH=60°EH=CH=BCsin60°=，•，∴EC=2CH=3，∴PA+PB+PC的最小值为3．3-1△PBQB60°△EBGPQ=EG△BQG（）如图③中，将绕点逆秒针旋转得到，则，是等腰三角形，第18页，共20页∴BQ=QGPQ=EG，，∴PQ+BQ+CQ=EG+GQ+QC≥EC，∴EC的值最小时，QP+QB+QC的值最小，-2BACDGADGOBOBP如图③中，延长交的延长线于，作△的外接圆⊙，将线段，B60°BQBEEOOBOP绕点逆秒针旋转得到线段′，，联接′，，．△BEO≌△BPOSAS易证′（），∴EO=OP′，APD+AGD=180°∵∠∠，APDG∴，，，四点共圆，∴OP=，∴EO=′，∴EO∴ECOEC点的运动轨迹是以′为圆心，为直径的圆，当点在线段′上时，的=CO-EO值最小，最小值′′，OOOOROR=OOBR∠OBR=90°RH⊥CB联接′，延长′到，致使′′，联接，则，作CBHOT⊥CHTOM⊥BCM交的延长线于，′于，于．Rt△OBMBM=5OM=在中，，，∴OB==，∴BR=OB=14，由△BHR∽△OMB，∴=，∴RB=4，HROTOMOO=RO∵∥′∥，′′，∴TM=TH，第19页，共20页∴O′T==，∴BT==3，∴CO==′，∴CO-EO=-=′′．∴QP+QB+QC的最小值为．1（）如图①，按照等腰三角形的判断和性质解决问题即可．2ABPBABPB60°BFEPFECBHEC（）如图②，将△绕点逆秒针旋转得到△，联接，，作⊥HPA+PB+PC=PC+PF+EFPC+PF+EF≥ECPFEC于．易证，由于，推出当，在直线上PA+PB+PCEC时，的值最小，求出的长即可解决问题．3-1△PBQB60°△EBGPQ=EG△BQG（）如图③中，将绕点逆秒针旋转得到，则，是等腰三角形，易知PQ+BQ+CQ=EG+GQ+QC≥EC，推出EC的值最小时，QP+QB+QC-2BACDGADGO的值最小，如图③中，延长交的延长线于，作△的外接圆⊙，将线BOBPB60°BQBEEOOBOP段，绕点逆秒针旋转得到线段′，，联接′，，．易证△BEO≌△BPOSASEO=OP=EO′（），推出′，推出点的运动轨迹是以′为圆心，ECOEC=CO-EO为直径的圆，推出当点在线段′上时，的值最小，最小值′′．本题属于四边形综合题，考查了旋转变换，全等三角形的判断和性质，等腰三角形的判定和性质，解直角三角形等知识，解题的关键是学会借助旋转法添加辅助线，构造全等三角形解决问题，学会用转化的思想思索问题，属于高考压轴题．第20页，共20页